(This is Part III for a multi-part series on “Logarithmic Distribution of Returns”. Read Part I HERE and Part II HERE.)
I come across the flaw of averages in reporting quite a bit. Take my article on MoviePass. The CEO said in an interview with The Indicator that the “average MoviePass customer sees 1.7 movies per month”.
If you read my articles from a few weeks back explaining distributions—and I know you read all 3,000 words—that average of “1.7” is virtually meaningless. He could have told us what the distribution looked like, but didn’t. And probably for good reason. (Impending bankruptcy.)
Since he won’t tell us, here are my guesses:
I would call this a “Log-ish” distribution. First, it’s not a continuous range. With MoviePass, they had discrete scenarios. You see one movie or two movies, but not 2.5. Also, my guess is more people use the service in a given month then let it sit idle, which keeps this from being a true log distribution. I also put an artificial cap at 10 films. That said, the behavior in general will have power-law results. (Some very small number of people will see an order of magnitude more movies over a year, literally 100 in some reported cases.)
(If these numbers were true—and I have no reason to expect them to be—then MoviePass would lose, on average, $5 per month per customer, on average. Given they had 3 million customers when I got my 1.7 number, this would put losses at 15 million per month. Since their CEO said that they were losing 21 million per month, my gut says that tickets were more expensive than my model, mainly because they were over-indexing on coastal users. Also, if the subscribers went up to 4 million, I’d be about perfect.)
Still, I found a Logarithmic Distribution in a random place. (Said in the voice of Rhianna to the tune of “found love in a hopeless place”.) When I started this three part series, I called the Logarithmic Distribution of Returns the “most important shape” in entertainment. I said it applied EVERYWHERE, not just to movies.
Well today, I’ll show you the everywhere. I’ll be blunt with you, I want to convince you of two things:
1. This is the reality of returns in every field of entertainment.
2. The average sucks (or is “sub-optimal”) at describing this reality.
Data Notes and Cautions
Some cautions on data, as always. Why do I always talk about the data itself? Like why provide this critique of my data? Because NO ONE else does on the internet. You should always be as informed, especially when coming with numbers, so when I use data I want you to know what I do and don’t have, what I can and can’t prove.
Caution 1: I’ve seen this in more places than I can share.
I worked at a streaming company, but that data is confidential so I can’t share it. In addition, I’ve done deep dives into other parts of entertainment, but sometimes I can’t find the charts I’d made, or they were on other computers. So that’s a bummer.
Caution 2: I’m limited by available data.
In many cases, I don’t have access to the database that has all the information. To really show a log-distribution, you need all the data, not just slivers. Instead, I have to rely on what I can find—the good graces of the internet—which is usually top ten, top 25 or top 50 lists, which isn’t good enough. We can still extrapolate using some logic, but if I had access to the database itself, it would all look more logarithmic.
Caution 3: I plan to update this over time.
This post has taken a lot of research, which takes time. At the same time, I promised this three weeks ago. So to manage both priorities, my goal is to post this today, then update it over time as I find more examples and/or think of more.
On to the examples.
Video
Or “filmed entertainment”. Any marriage of visual recording with audio usually performs like our logarithmic returns. But let’s start with our example from last time.
More Movies/Films
As a reminder of a perfect logarithmic distribution, here’s box office returns in 2017.
In my second article, I showed how this distribution applied to multiple genres of films. Well, I recently looked at this for another genre of films. And guess what? We got the same distribution. In this case, I looked at war films.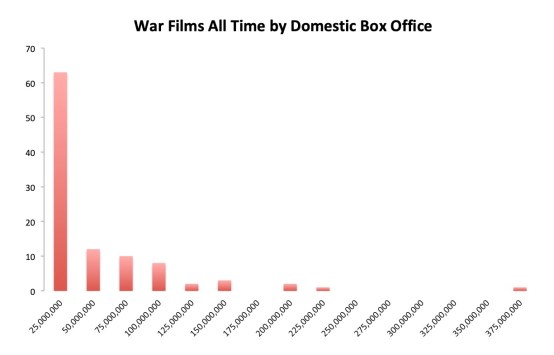
Source: Box Office MoJo
TV Ratings by Series
Of course, you could argue that maybe theatrical box office skews the performance of video. So let’s turn to the other primary form of video, TV. Let’s start with traditional broadcast TV. Deadline had a summary of the ratings for broadcast channels in 2017 with the top ratings by series. Unfortunately, it doesn’t look as great as I wanted:
Source: Nielsen, via Deadline
What went wrong? Well that’s “broadcast” TV. In fact, that’s broadcast “prime time” TV. People with cable (or broadcast) can watch a lot of other types of shows: daytime programming, syndicated shows and cable. Oh, all the cable.
In a future update, my goal is to expand this table. (Trust me I’ve google the internet for a while and this is the biggest hold up to me posting today.) If I had access to Nielsen, I could do make the table pretty quickly. Instead, they only provide “Top 10s” and I can only find prime time broadcast on publicly available sites. (I made this chart for work before with Nielsen data.)
So I’m not off to a great start (though trust me, if you add cable above it looks logarithmic), but I have two other TV options to show.
TV Channels Viewership
Of course, we could also look at “TV Channels” as their own distinct entities. Do we get the same type of performance? I hadn’t initially thought of this, but stumbled across ratings by network when I was looking for data in my “CBS Myths Debunked” article. Here you go:
Source: IndieWire
TV Subscriber Fees
Thinking of channels got me to think of another way to measure the value of TV channels, by the amount cable companies have to pay in “subscriber fees”. I don’t have time to explain sub fees now, but just know they were the straw that stirred the drink for the last few decades in cable. I had some old data from 2012 listing cable sub fees and here you go:
You could look for logarithmic distribution in “total subscribers” in cable, but you won’t find it. There is a cap on the number of households that can subscribe to a cable channel, which nears the total number of households at 100 million-ish. As a result, when cable channels hit that upper limit, they used fees to capture the extra value.
Streaming
So Netflix, Amazon, Hulu and the rest don’t share ratings data. So no charts here. But I’ve seen the data for one of the streamers, made the charts, and let me assure you this: this law absolutely applies. The most popular shows on a streaming platform are multiples bigger than the vast majority that come, go and are forgotten. If anything, given the larger sizes of the platforms, the effects of the log-distribution are more pronounced.
Speaking of size of libraries, let’s head to the largest library of video on the internet.
Youtube
Know this: if you search for information on the number of views by video, you find a lot of articles on “Gangnam Style”. Which I’m not saying to be negative, just pointing out.
Search hard enough, and I did, and I found the key insight here. This long, information article on a website called the The Art of Troubleshooting, where he used some scraping and R to pull the data on the video views. I took a screenshot of his “log-normal distribution” of video views. (In other words, he converted the logarithmic distribution into “logs” to show the normal distribution. It’s the same thing, it just looks different because the scale is in log.)
Here’s the picture and another link to his site.
Source: Art of Troubleshooting
The insight with Youtube makes sense: “Despacito” and previously “Gangnam Style” have literally billions of views. Yet, since anyone can make a video, the vast, vast majority have 0-100 views. This effect continues with channels as well, as measured via subscribers, sort of like how I measured both by show and channel above. This article on Vox has some of the statistics showing how big the biggest stars are. For example, PewDiePie is way out front, but most people don’t have any subscribers to their channel.
Youtube is definitely winner-take-all and the distribution holds. Here’s a chart showing the top 250 channels by sub. Look at the trend:
Source: TwinWord
If we turned this into a histogram and expanded it out, we’d get our log distribution.
Social Media & The Internet
As the Youtube example shows, as the sample size grows, the effects of the power-law get amplified. Moreover, with the internet, the data is a bit easier to come across. And it makes the power-law distribution even starker.
Social Media
Let’s start with Twitter. Do the number of followers someone has follow a power law?
Source: StatisticsBlog.com
According to this website, yep. And again this makes sense: Rinaldo has tens of millions of followers while most people are in the hundreds and bots have hardly any. This other article says that over 90% of people have less than 100 followers, which makes sense. Let’s head to Facebook. In this case, the number of friends someone has is NOT power-law, since it isn’t really consumer facing. But, the number of likes something has does follow this law:
Source: A ScribD article via Quora
In the future, I could look at both measurements of fandom (subscribers, followers, etc) or popularity of individual posts (likes, shares, etc) on multiple other social platforms and you get the same effect each time. That’s what going viral is.
Internet
One last part of this which is how the internet started: old fashioned webpages. Do certain cites have multiples more viewers? Of course.
Source: Top News Sites via Statista
That comes from Statista, who only covered news websites. You can go to Alexa and see another list of top websites, all in the hundreds of millions of monthly visitors. Yet, according to this one website, there are 1.89 billion websites. That’s definitely power law distribution. This random paper online backs this up.
Next Time
So that’s five pages, 12 charts, and 7 or 8 different categories of entertainment (film, war films, TV shows, TV channels, Twitter, Facebook and the internet).
But I’m not done, just done for today. In my next update, I’ll try to tackle music—there are two more databases I don’t have access to—and other more unique/weird subsets like toys, comic books, sports and theme parks.
